皆さまこんにちは。前回は“問題解決実践編”として、“社内で眠っているデータの徹底活用”について書きました。前回投稿の中で、“ロジスティック回帰分析”について今後書いてみたいと思います、と書きましたが、今回はその“ロジスティック重回帰分析”について、書いていきたいと思います。
“ロジスティック回帰分析”とは?
前回投稿の中では、下記のようなデータを使って、重回帰分析をしようとしていました。
性別
年齢
年代
未既婚
居住地
知っているプライベートブランド(複数選択)
プライベートブランド別のイメージ(複数選択)
ここ1~2年での、プライベートブランドの購入頻度の変化(増えた・減った・変わらない)
上記の理由(自由回答)
この1年以内に、プライベートブランドに切り替えた食品(複数選択)
この1年以内に、プライベートブランドに切り替えた調味料(複数選択)
この1年以内に、プライベートブランドに切り替えた飲料(複数選択)
この1年以内に、プライベートブランドに切り替えた医薬品(複数選択)、等々
上記データの中で、結果変数となりそうなのが、まず“ここ1~2年での、プライベートブランドの購入頻度の変化(増えた・減った・変わらない)”で、また“この1年以内に、プライベートブランドに切り替えた食品/調味料/飲料/医薬品”も使えそうでした。
“ここ1~2年での、プライベートブランドの購入頻度の変化(増えた・減った・変わらない)”は(1/2/3)、“この1年以内に、プライベートブランドに切り替えた食品/調味料/飲料/医薬品”は(0/1)といった選択式の回答結果で、これらは離散変数と呼ばれます。
前回はエクセルで重回帰分析をしたかったので、離散変数から連続変数のカラムを作って分析を進めました。エクセルでの重回帰分析は“線形回帰分析”といって、結果変数は連続変数しかとれないのでしたよね?
今回は、上記の離散変数を結果変数としてそのまま分析できる“ロジスティック回帰分析”を取り上げます。
“重回帰分析“と“ロジスティック回帰分析“の違い
重回帰分析(線形回帰分析)では、説明変数xが結果変数yの値を変化させます。そのため、説明変数から、結果変数の「値」を予測可能です。一方、ロジスティック回帰分析の結果変数は離散変数なので、“1/0”の形(特定の現象の有無)です。つまりyが1になる確率を判別します。結果変数が離散変数の場合に重回帰分析(線形回帰分析)を用いた場合、分析できないことはなく、それらしい結果が出力されることもあるかと思いますが、必ずしも正しい結果とは限らないので、注意しましょう。
それでは下記で、“ここ1~2年での、プライベートブランドの購入頻度の変化(増えた・減った・変わらない)”を結果変数として、ロジスティック回帰分析をやってみます。
“ロジスティック回帰分析”の手順
重回帰分析(線形回帰分析)と違い、ロジスティック回帰分析はエクセルではできないので、今回はロジスティック回帰分析も可能な統計ツール“R(無料ツール)”を使ってみます。Rは他にも重回帰分析(線形回帰分析)や決定木分析、クラスター分析等様々なデータマイニング(統計分析)手法を扱うことができるとても便利なツールです。Rそのものについてはググるとたくさん記事が出てくると思いますので、ここでは書きません(参考までに、一つだけリンクを貼っておきます)。
Rを使うには色々なやり方がありますが、今回は“Google Colaboratory(以下、コラボ。これも無料!)”を使ってRを動かすやり方で進めます。コラボそのものについてもググるとたくさん記事が出てくると思いますので、ここでは書きません(参考までに、一つだけリンクを貼っておきます)。
コラボにアクセスしたら、まずメニューバーの「ファイル」→「ノートブックの新規作成」と進みます。
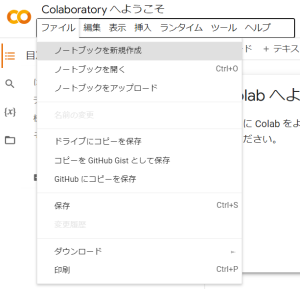
次に、またメニューバーの「ファイル」→「ダウンロード」→「.ipynbをダウンロード」と進みます。

ダウンロードした”.ipynb”ファイルを、メモ帳等のテキストエディタで開きます。

赤枠で囲った部分の “name”: “python3”, “display_name”: “Python 3″ を、”name”: “ir”, “display_name”: “R” と書き換えて保存します。

コラボの画面に戻って、またメニューバーの「ファイル」→「ノートブックをアップロード」と進み、先ほど保存した “.ipynb”ファイルを選択します。

メニューバーの「ランタイム」→「ランタイムのタイプを変更」を選択します。

表示されたダイアログボックス内、“ランタイムのタイプ”が“R”となっていればOKです。これでコラボ上でRを実行する準備ができました。

まず分析するデータファイルを読み込みます。画面左側フォルダマーク(図8内の吹き出し1)をクリックし、次に上向き矢印(図8内の吹き出し2)をクリックして、ファイルを選択します。
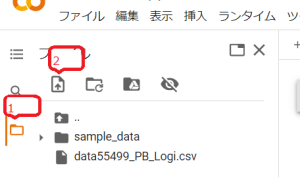
ファイルが読み込めたら、いよいよロジスティック回帰分析を実行します。
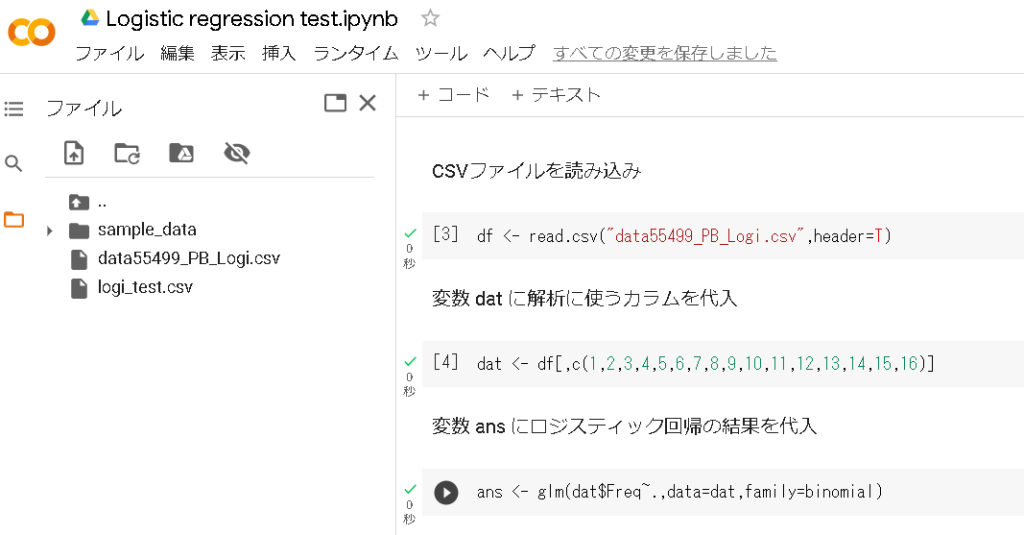
図9でやっていることは、下記の通りです。
1. データ(Rに読み込んだCSVファイル)を変数”dat(変数名は何でもいいです)“に読み込み
2. 1.で読み込んだデータから、分析に使用するカラムの指定
3. ロジスティック回帰分析の実行(右側の”glm”がロジスティック回帰分析のコマンド。ここでは実行結果を、変数“ans”に読み込んでいます)
分析結果の見方
それでは分析結果を表示してみましょう。

真ん中辺りに “Coefficients:”と書かれた表があります。左から”Estimate”, “Std.Error”, ”z value”, “Pr(>|z|)”と並んでいます。この中の “Estimate” が、線形重回帰分析で出てきた “Coefficient (係数)”と同じで、”Pr(>|z|)”が”P値”です。見方は線形重回帰分析と同じで、P値が5%未満で、より大きい係数が、より結果変数へのインパクトが大きいということになります。この中で見ると”Price(プライベートブランドを購入する際に重視すること -【価格】)“、”Foods(この1年以内に、メーカー品からプライベートブランド商品に切り替えた食品数)“の順にインパクトが大きいですね。
ここでロジスティック回帰分析の場合は、もうひと手間かける必要があります。重回帰分析の場合は、Y=ax1+bx2+cx3…+dという式を作るのでしたね。Yが結果変数だったので、係数(上記式内のa,b,c)を変えることで、Yを予測することができました。
ロジスティック回帰分析の場合、結果変数は離散変数で1/0の形になっています。なので、この1になる割合を考えることになります。式で表すとこのようになります。
log(p/1-p) =ax1+bx2+cx3…+d
pが1になる割合で、1-pは1にならない割合です。この比率はオッズ比と言われるものです。聞いたことはある方が多いのではないかと思います(参考)。ロジスティック回帰分析は、このオッズ比に与える各説明変数のインパクトをモデル化しているのですね。
ではRで、このオッズ比に与える各説明変数のインパクトを算出してみます。

Expがオッズ比を出すコマンドで、その引数として、先ほどロジスティック回帰分析の結果を入れた変数を入れています。先ほど同様(上記図10参照)、左から”Estimate”, “Std.Error”, ”z value”, “Pr(>|z|)”と並んでいますが、数字は異なっていますね。この “Estimate”列に入っている数字が、オッズ比へのインパクトの大きさになります。
先ほど同様、”Price(プライベートブランドを購入する際に重視すること -【価格】)“、”Foods(この1年以内に、メーカー品からプライベートブランド商品に切り替えた食品数)“の順にインパクトが大きいのですが、今度はこの数字がこのまま使えます。Priceは2.43..なので、この変数が1増えると、”プライベートブランドの購入頻度が増えたかどうか”が1になる確率(オッズ比)は2.43倍、Foodsは同様に2.29倍、、という見方になります。
以上、ロジスティック回帰分析でした。線形重回帰分析よりひと手間増えるものの、無料ツール(コラボ&R)で実行できますし、これを覚えれば、結果変数が連続変数でも離散変数でも対応できるようになりますので、ぜひ問題解決者としてレパートリーに加えてみてください!
今回はこのくらいにさせていただき、また次回以降、続けていきたいと思います。 最後まで読んでいただき、ありがとうございました。