皆さまこんにちは。前回は問題解決にあたって“一次調査(独自調査)”をする際の分析手法の1つとして“狩野モデル”について書きました。今回はまた別の分析手法である“重回帰分析”について、書いていきたいと思います。
1. “重回帰分析”とは?
重回帰分析とは、統計分析の手法で、いわゆる“多変量解析”と言われる手法の1つです。エクセルのようなスプレッドシートのデータですと、縦軸が“行”、横軸が“列”になりますが、この“列”が複数ある時に、重回帰分析を使うことで、特定の列に対する影響度が大きい列が分かります(例:“顧客満足度”に影響が大きい要因⇒“提案力”、“価格”、等)。
古くは“データマイニング”、最近だと“データサイエンス”とか言われる分野の1手法、とも言えるかと思います。これらの手法は本当に星の数ほどもあって、また流行り廃りもありますが、この重回帰分析は古くからあって、使いやすいので、私もよく使っています。どんな点で使いやすいのかと言うと、a) 汎用性、b) 結果が明快、c) ステークホルダーに説明しやすい、の3点があると思います。
a) 汎用性
重回帰分析は、割と色々なデータを分析することができます。分析手法によっては、データを集める前段階(調査設計段階)からしっかりデザインしないと使えない、というものもありますが、重回帰分析の場合は、“手元にこんなデータがあるんだけど、何か使えないかな”というような場面でも力を発揮します。
スプレッドシートのデータですと、この“列”が複数あって、数値化されていれば使える場合が多いです(大雑把に言うとですが)。なので、色々なプロジェクトで、社内の色々な部門とやり合う“問題解決者”の皆さまにはとても心強い味方である、と言えると思います。あと統計専用ツールではなく、“エクセルでそのまま分析できる”というのも助かりますね!(Googleスプレッドシートもアドオン”XLMiner Analysis ToolPak”を導入することで、ほぼ同様の分析ができます)
b) 結果が明快
分析手法によっては、分析結果を分析者が解釈して軸に名前を付けたりとか、分析者の主観が入るような手法もありますが、重回帰分析は結果自体はとてもデジタルに出てきます。ので見方さえわかっていれば、主観の入る余地が少ないので、この点もいいと思います。
c) ステークホルダーに説明しやすい
これは“問題解決者”の皆さまが、この手の分析手法を使うにあたって、かなり大事なポイントだと思いますので、また後で触れます。
2. “重回帰分析”のポイント
具体的な分析の進め方はたくさんネットに出ていますので、いつものように1つだけリンクを貼らせていただきます(データのじかん様記事)。こちらのリンク先にもあるように、分析の実行自体はエクセルで一瞬で終わります。以下、2点だけポイントを書いてみます。
①分析前の準備:欠損値の取り扱い
データの中に空欄が混ざっていることはよくあると思います。この空欄を“欠損値”と言います。欠損値が入っていると重回帰分析がうまく実行できないので、欠損値を取り除く必要があります。取り除き方も色々あるのですが、“実践的”な方法は2つです。
1つは欠損値を含んでいるレコード自体を削除することです。このやり方の問題点はデータのサンプル数が減ってしまうことで、サンプル数が潤沢でないデータ(100件以下くらい)の場合はお勧めしません。
2つ目は、空欄がある列の平均値を算出して、空欄に入れるやり方です。
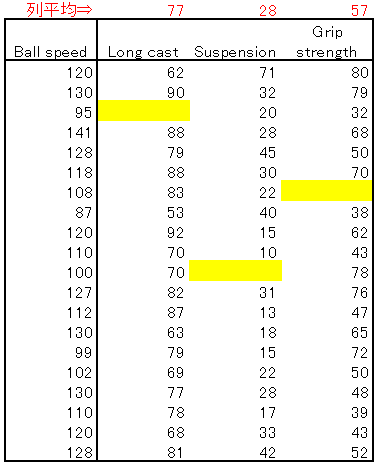
このやり方ですと若干データのバラつきは変わりますが、平均値は変わらないのでデータの分布への影響は少なくできます。何より簡単なのがいいですね。
あともう1つ、分析前の準備として大事なものに”多重共線性”のチェックがあります。これは説明変数(上記表の例で言うと”Long Cast”, “Suspension”, “Grip strength”の3列)間で相関関係が強いとうまく分析ができなくなってしまうことです。回避方法についてはこちらをご覧ください。
②分析結果の読み方
エクセルで重回帰分析を実行すると、このような表が出力されます。色々な項目が出てきて何が何やら、、となるかもしれませんが、見る必要がある項目は3つだけです。
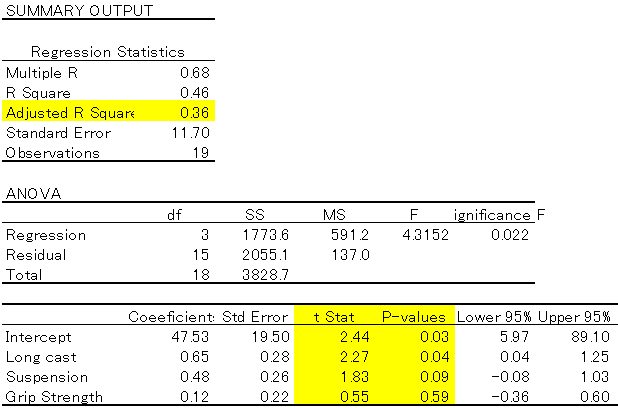
Adjusted R Square(日本語版エクセルだと“補正R2”となっている)
”Multiple R(重相関R)“、”R Square(重決定R2)“と並んでいますが、重回帰の場合はここを見ましょう。結果変数(この例だと”Ball speed”)のバラつきの何%がこの分析で説明できているか、という値です。100%に近いほど良い、という見方です。
T-stat(日本語版エクセルだと”t”となっている)
結果変数への影響の大きさ。2以上の数値を見るようにする。”Coefficient(係数)“も影響の大きさを表しますが、こちらは単位によって変わってしまうことがある(1mと100cmでは結果が変わる場合がある)ので”T-stat”を見るのが良いと思います。
ただ“Coefficient(係数)”も、下でも書いていますが、予測に使えるので大事です。上記の例で言うと、Y (Ball speed) = 0.65×1 (Long cast) + 0.48×2 (Suspension) + 0.12×3 (Grip strength) + 47.53 となります。この予測式は、例えば”Long cast (遠投)”が1m伸びると、Ball speedは0.65km速くなる、という意味です。
P value(日本語版エクセルだと”P-値”となっている)
5%未満のものだけ見るようにする。偶然によってバラつきが生じる確率で5%以上だと偶然の可能性が高い、という見方になります。
3. ステークホルダーへの説明の仕方
先ほども書きましたが、“問題解決者”である皆さまは、分析結果をプロジェクトのステークホルダーに説明して理解してもらうことが大事です。重回帰分析のような高度な統計手法を使うと、この部分がネックになることがよくあるので、説明の仕方を準備しておくことが重要になると思います。
よく聞かれるのが“相関分析との違い”です。相関も重回帰と同様に、複数の列を含んだデータを分析しますが、相関でわかるのは列間の関係性の強さです(0.3だと弱い、0.8なら強い、等)。
それに対して、重回帰分析は因果関係を示しています。重回帰分析は、要は昔数学で習ったY=ax1+bx2+cx3…+dです。Y=結果変数、a, b, c=Coefficient(係数、説明変数と言ったりもする)、d=Intercept(切片)、ですね。これは何を言っているかというと、係数を変えることによって結果変数の予測ができるということなのですね。これが相関との大きな違いであると言えます。まずはここを抑えておくと良いと思います。
ちなみに今回取り上げた重回帰分析は、厳密には線形回帰分析と呼ばれるもので、目的変数が連続変数である必要があります。目的変数が離散変数の場合、ロジスティック回帰分析を使う必要があります。ロジスティック回帰分析については、こちらをご覧ください。
今回はこのくらいにさせていただき、また次回以降、続けていきたいと思います。 最後まで読んでいただき、ありがとうございました。